В этом модуле вы узнаете, что такое отложенное окно конверсии; какие ошибки можно допустить, если поспешно принять решение по итогам эксперимента; как смотреть различия в выборках; как использовать Python для анализа результатов теста: библиотеки Pandas и Seaborn для анализа данных и их визуализации.

Мы собрали необходимое количество данных и остановили эксперимент. Кажется, что самое время выгружать их и интерпретировать результаты теста. Но не все так просто!

Окно конверсии

Сначала вам надо убедиться, что так называемое окно конверсии закрылось для всех участников эксперимента.

Окно конверсии — это временной период, в течение которого мы наблюдаем за пользователем в ожидании, что он совершит целевое действие.

Для примера снова обратимся к одной вымышленной онлайн-школе. Допустим, мы тестируем решение для повышения конверсии из регистрации в оплату. Эксперимент, согласно нашему дизайну, шел 14 дней. На 15-й день мы остановили A/B-тест, выгрузили данные контрольной и тестовой групп. Мы знаем, что в среднем пользователю требуется 5 дней на принятие решения об оплате. Давайте порассуждаем вместе:

• Сколько дней на то, чтобы совершить оплату, было у учеников, которые попали в эксперимент в первый день? Больше 13.
• Сколько дней на принятие решение было у учеников, которые попали в наш эксперимент в последний день теста? Меньше одного.
• Что будет, если мы начнем подводить результаты A/B-теста на 15-й день? Мы срежем часть конверсий, которые могут изменить финальное решение об успешности нашей гипотезы.

Следовательно, выгружать данные и начинать анализ результатов A/B-теста можно только тогда, когда окно конверсий закрылось для всех пользователей, попавших в наш эксперимент.

Как определить окно конверсий? Перед запуском эксперимента нужно проанализировать исторические данные. Хорошая практика в данном случае — воспользоваться 95-м перцентилем, то есть взять в качестве окна конверсии период времени, за который целевое действие совершает 95% всех пользователей.

Помните, что выгружать данные для анализа можно, только когда с момента завершения эксперимента пройдет период времени, равный окну конверсии.

Проверка на выбросы

Перед подведением результатов рекомендуем также проанализировать данные по дням. Иногда накопленная разница между вариантами в эксперименте может объясняться аномальными выбросами нашей ключевой метрики в один или несколько определенных дней.

В идеальной картине следует определять понятие «выброса» при проектировании эксперимента. Довольно часто для этого прибегают все к тем же перцентилям: аномалиями считают значения, лежащие за 1-м и 99-м перцентилями. Не факт, что они искажают результаты вашего теста, но проверить точно стоит.

Универсальных правил по работе с выбросами нет, все решается индивидуально, но важно, как минимум, провести расследование, с чем связан аномальный рост или падение метрики в конкретные дни. Это может быть что угодно: техническая проблема, активность конкурентов, неизвестная вам маркетинговая акция. По результатам расследования в зависимости от природы выброса нужно будет принять решение: исключить из анализа наблюдения, собранные в аномальный день, или нет.

Проверка равномерности распределения

При подведении итогов A/B-теста гигиеной является проверка на распределение различных сегментов пользователей между тестовой и контрольной группой.

Это крайне важно, так как разница между вариантами может возникнуть из-за того, что в одну из выборок попадет больше пользователей, склонных к совершению целевых действий. Например, вы развиваете премиальный продукт на российском рынке и решили провести эксперимент, в основе которого лежит гипотеза для роста конверсии в оплату.

В тестовую группу по какой-то причине попало больше пользователей из Москвы. А они более платежеспособны, чем пользователи из регионов, где средний доход ниже. В результате вы можете сделать ошибочный вывод, что ваша гипотеза верна, в то время как благодарить за такой расклад можно только особенности централизованной экономики.

Примеры сегментов, которые важно проверить

• По каналам привлечения.
• По географии.
• По времени жизни в сервисе.
• По платформе.

А лучше вообще мониторить распределение в реальном времени в процессе теста.

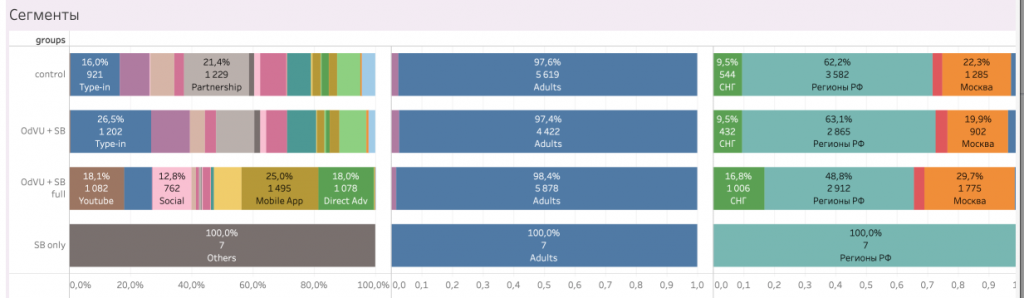
Если вам известны другие характеристики пользователей, которые могут влиять на вероятность совершить целевое действие, то смело дополняйте список. Например, в Skyeng мы дополнительно проверяем сегменты учеников по уровню знания языка и по возрасту или классу школьников.

Если пользователи в ваших выборках оказались распределены неравномерно, то это снова повод провести расследование. В целом, это не безнадежная ситуация, так как выводы по эксперименту можно будет сделать с помощью приведения структуры пользователей в одной группе к структуре из другой группы. Это снизит точность, но может спасти драгоценное время.

Анализ результатов

Приближаемся к самому интересному. Если упростить, то для подведения итогов A/B-теста нам будет необходимо:

1. Проанализировать характер распределения полученных данных.

2. Выбрать статистический критерий.

3. С помощью статистического критерия ответить на вопрос, есть ли между вариантами значимая разница.

Мы уже касались первых двух пунктов при проектировании экспериментов, но, как и обещали, разберем их детальнее. Ух, сейчас будет немного диванного матстата, не заскучайте!

Напомним, что статистический критерий — это математическое правило, которое помогает нам понять, принята или отвергнута наша гипотеза. У каждого критерия есть предпосылки для его использования. Критерии могут работать неправильно, если этими предпосылками пренебречь. Например, для некоторых критериев может быть недопустимо, что данные распределены ненормально, есть много повторяющихся значений или сам объем выборки невелик. Крайне рекомендуем перед расчетами всегда проверять, соответствуют ли ваши данные предпосылкам, иначе мы можете получить неверный результат проверки. Пример того, как важно правильно подобрать статистический критерий, можно изучить в статье Виталия Черемисинова на Medium.

Работа статистического критерия заключается в подсчете некоторой статистики (у каждого критерия она своя) на основе полученных данных. Зная теоретическое распределение этой статистики, мы можем рассчитать вероятность понаблюдать полученное значение статистики — или еще более экстремальное, при условии верности нулевой гипотезы. Эта вероятность называется p-значением и дальнейшее решение относительно отвержения нулевой гипотезы принимается на основе сравнения полученного p-значения с установленным в дизайне эксперимента порогом (уровнем значимости).

Статистические критерии разделяют на параметрические и непараметрические.

Параметрические включают в расчет какие-то параметры вероятностного распределения признака, например, среднее значение или дисперсию.

Непараметрические, напротив, не включают в расчет параметры распределения и основаны на оперировании частотами или рангами.

Если мы знаем закон, согласно которому распределена метрика, то можем воспользоваться параметрическими методами. В остальных случаях оперировать можно только непараметрическими критериями. Поэтому первым делом мы рекомендуем всегда определять характер распределения. Но сначала вспомним, что же такое распределение и каким оно может быть.

Виды распределений

Каждое значение какой-либо метрики может случиться с определенной вероятностью. Например, сумма заказа в 3 тысячи рублей встретится чаще, чем сумма заказа в 300 тысяч рублей. То, с какой частотой и какие значения может принимать метрика, и определяет ее закон распределения.

Вы наверняка слышали про нормальное распределение (или распределение Гаусса). Оно является одним из самых важных в статистике. Простыми словами его значимость можно описать так: величины, которые складываются под воздействием большого числа мелких независимых факторов, часто будут подчиняться нормальному закону распределения (если хочется чуть подробнее, почитайте про центральную предельную теорему на Википедии). Благодаря этому многое в природе распределено нормально или близко к нормальному распределению: рост, вес, уровень знаний, ошибки наблюдений, скорости молекул в объеме газа.

График плотности вероятности нормального распределения имеет форму колокола.

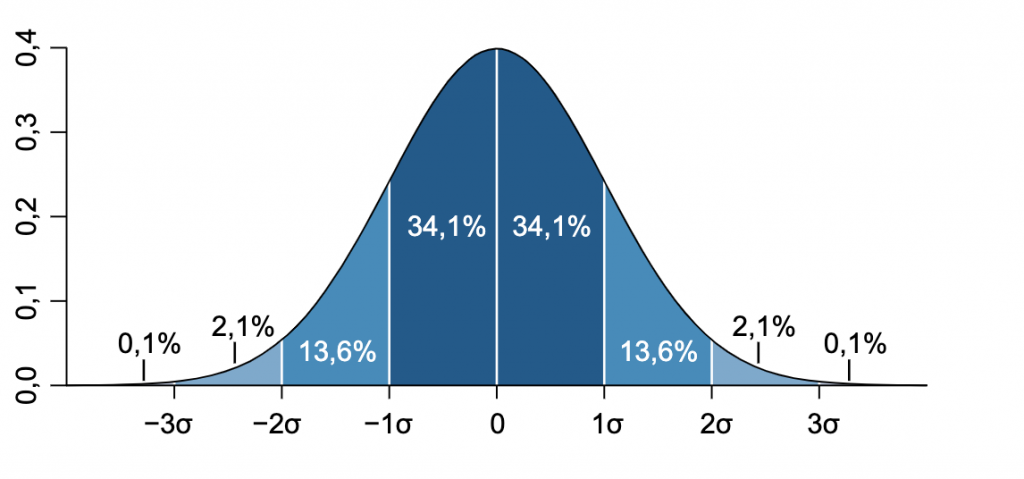
Благодаря такой форме у нормального распределения есть ряд «удобных» свойств: среднее значение находится в центре колокола, практически все значения находятся в интервале ±3 стандартных отклонений от среднего (это свойство еще называют «правилом трех сигм»). Распределение симметрично, поэтому, например, в группе со средним ростом 175 см с одинаковой вероятностью можно найти человека с ростом 160 и 190 см.

Еще один ваш друг в мире статистики — биномиальное распределение. Оно описывает «успехи» в последовательности из независимых случайных экспериментов. Вероятность «успеха» в каждом из них постоянна и равна какому-то значению p. В качестве «успеха» мы рассматриваем некое действие пользователя: клик, добавление товара в корзину, покупку. Если действия отдельных пользователей независимы (как чаще всего и бывает), то их можно описать законом биномиального распределения.

Как определить характер распределения

Проверить распределение выборки довольно просто — статистика предлагает нам ряд методов. Для начала постройте гистограмму своих данных. Уже по ней вы сможете понять, есть ли возможность использовать критерии с предпосылками о нормальности распределения выборки.

Несколько примеров

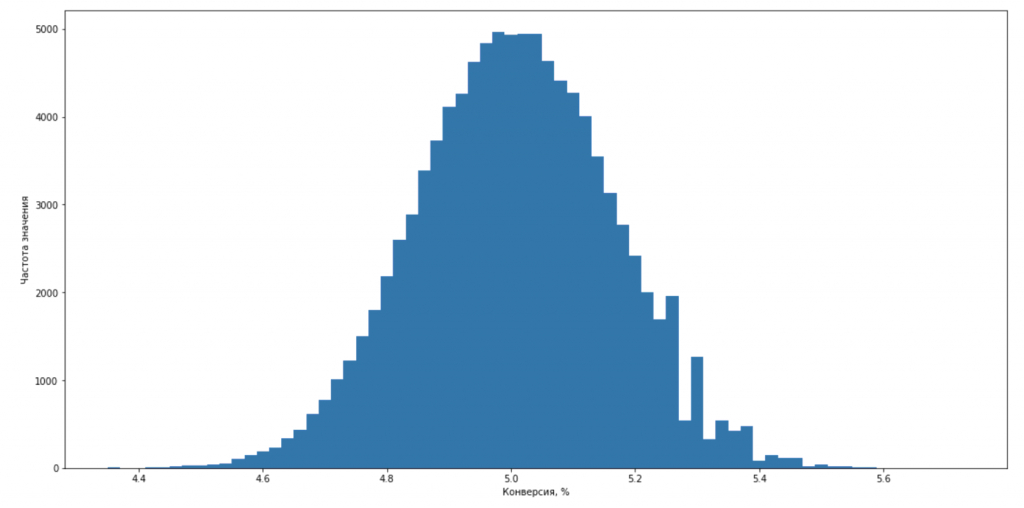
• Метрики конверсий имеют биномиальное распределение. Для них подойдут и параметрические, и непараметрические методы.

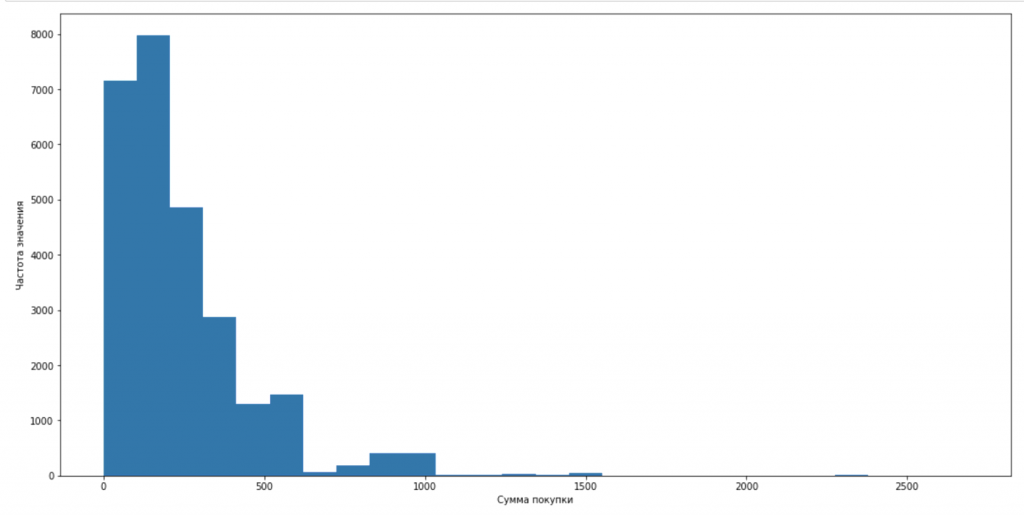
• Метрики, связанные с деньгами, чаще всего «скошены влево» — есть много пользователей с небольшим чеком и редко встречаются заказы с большой суммой. Анализируя их, вы чаще всего будете использовать непараметрические критерии.

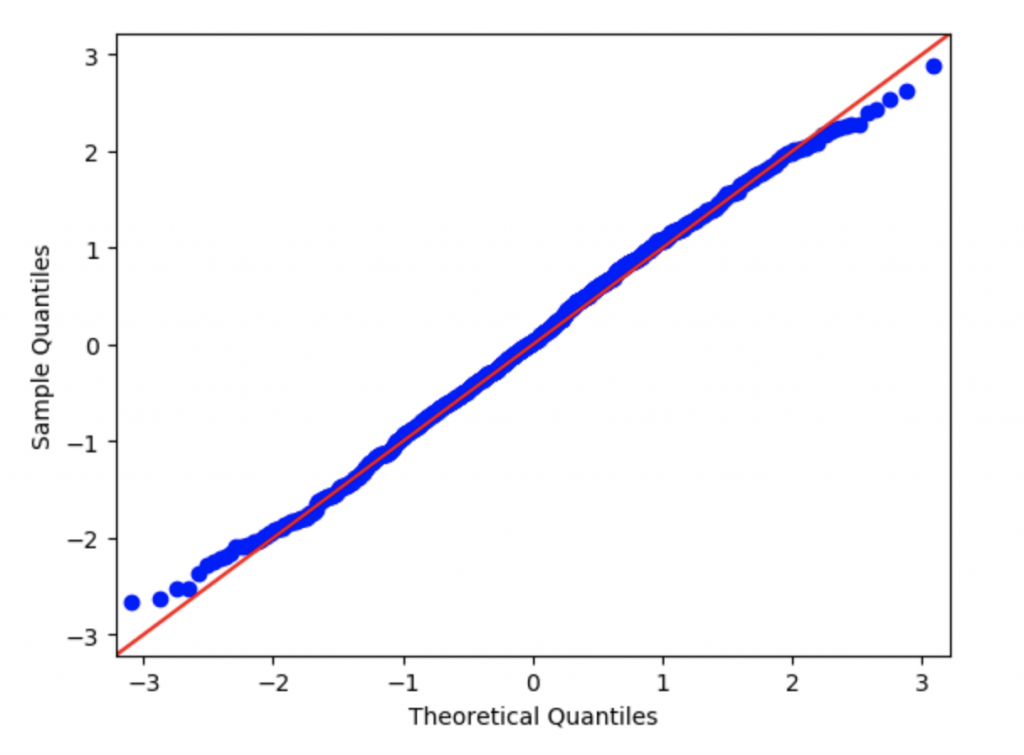
Еще один инструмент — это график квантиль-квантиль (Q-Q plot). Это тоже графический метод анализа, который позволяет сравнить два распределения, сопоставляя их квантили. По одной оси — значения квантилей выборки из эксперимента, по другой — значения квантилей теоретической функции распределения.

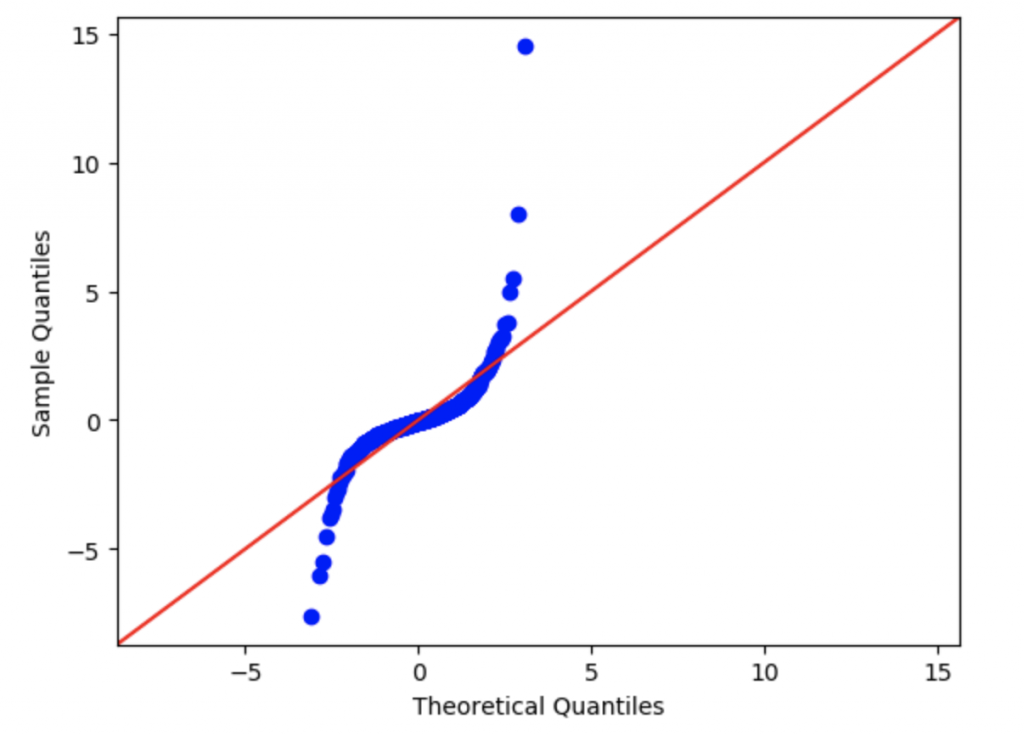
Если точки образуют прямую под углом 45 градусов, значит, выборка соответствует теоретическому распределению.

В противном случае — не соответствует.

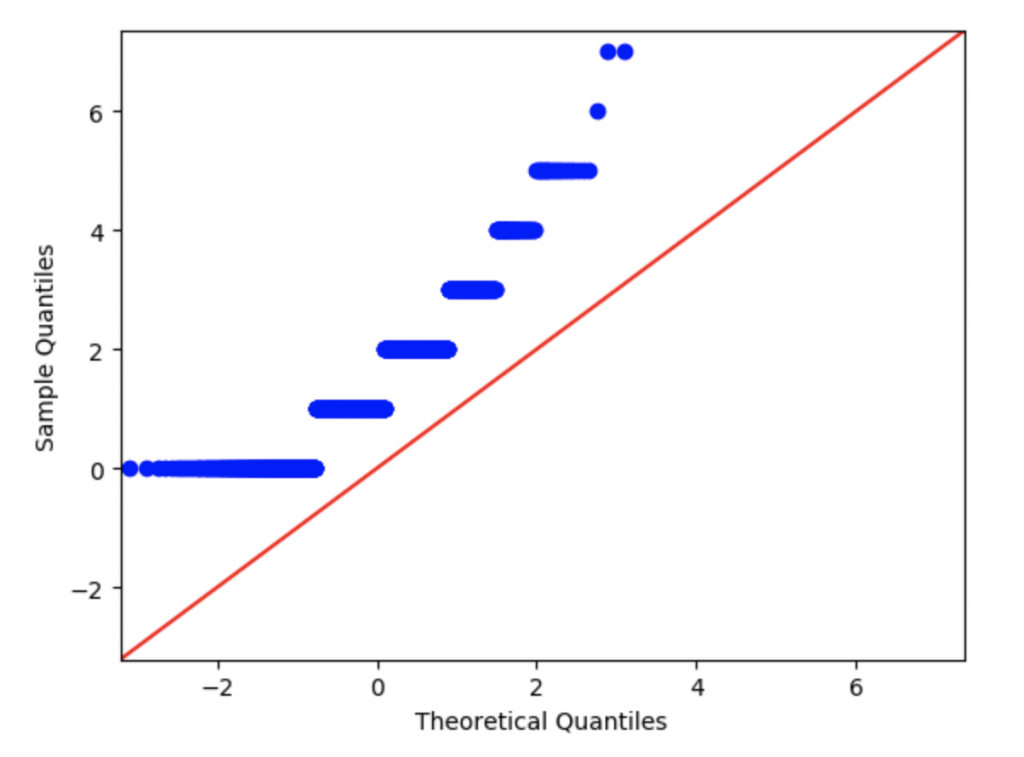
Дискретные выборки будут иметь характерный «рваный» график.

Если графического анализа недостаточно, вы можете использовать подходящий критерий согласия, который позволяет проверить соответствие эмпирического распределения (выборки из эксперимента) теоретическому распределению вероятностей. Во второй части домашнего задания мы научимся определять распределения с помощью кода на Python.

Как выбрать статкритерий

Чаще всего для нормально распределенных (или близких к нормальному распределению) выборок используется t-критерий Стьюдента для сравнения двух средних значений. Его статистика представляет из себя разность средних, специальным образом отнормированную на дисперсию, «шум». Именно из-за такой формулы критерий Стьюдента может выдавать неправильные результаты для выборок с другими законами распределения. Для интуитивного понимания: ошибка похожа на то, как если бы с помощью среднего арифметического мы пытались описать «скошенные» выборки с большим числом отклоняющихся значений.

Если вы анализируете конверсии или другие доли, вам понадобится критерий хи-квадрат (или критерий согласия Пирсона). Этот метод позволяет оценить статистическую значимость различий двух или нескольких относительных показателей (частот, долей).

Популярным в анализе A/B-тестов является непараметрический bootstrap. Работа метода заключается в многократном повторении (resampling) полученных данных путем формирования независимых подвыборок с возвращением, размер которых равен размеру исходной выборки. Что такое «подвыборки с возвращением» проще объяснить на примере.

Представим, что у вас есть 3 мяча с номерами 1, 2, 3. Вы кладете их в мешок, затем случайным образом достаете один из них, записываете на доску номер и кладете мяч обратно в мешок (поэтому — «с возвращением»). Далее вы снова случайным образом достаете мяч и повторяете процедуру. После трех шагов на доске может оказаться как комбинация 2-1-3 , так и 3-1-3, несмотря на то, что в исходной выборке мяч с номер 3 у вас единственный.

С возвращениями разобрались, давайте обратно к bootstrap. Для анализа эксперимента нам понадобится:

1. Для каждой группы (тест и контроль) сформировать подвыборку с возвращением.

2. Для каждой полученной подвыборки вычислить рассматриваемую в эксперименте метрику, например, средний чек или конверсию.

3. Вычислить разность полученных на втором шаге метрик между тестом и контролем.



С помощью многократного повторения шагов 1−3 с сохранением результата шага 3 формируется эмпирическое (то есть то, которое случилось на практике, а не в теории) распределение разности метрик. С помощью этого распределения можно вычислить p-значение или найти доверительный интервал для разности метрик с помощью взятия квантилей от полученного массива разностей. Попадание нуля в доверительный интервал будет означать отсутствие значимых отличий между группами.